Capacitors in Series and Parallel, Charge Buildup and Decay in Capacitors, A Capacitance Puzzle, Quantitative Measurements on an RC System

Capacitors in Parallel

Capacitors in Series and Parallel

capacitors in series

Two capacitors of the same capacitance ( .1E-06 F) were connected first in parallel and then in series.  When the capacitors were hooked up in parallel with alligator clips, a multimeter was used to measure the capacitance which was 1.945E-06 F while the capacitance hooked up in series was measured with the multimemter to be only .482E-06 F.  The relationships can be seen between capacitors connected in series and in parallel (see whiteboard)

Charge Buildup and Decay in Capacitors

A capacitor, a source of voltage, and a light bulb were all connected in series.  First the light bulb was lit and then as the capacitor was charged the light bulb dimmer and dimmer until it turned off.  Then the connections were taken out of the voltage source and touched to one another to create another series circuit but without the voltage source.  The light bulb lit up and the went dimmer and dimmer until it went out.  The light bulb was able to light up without the voltage source because the capacitor was charged with energy.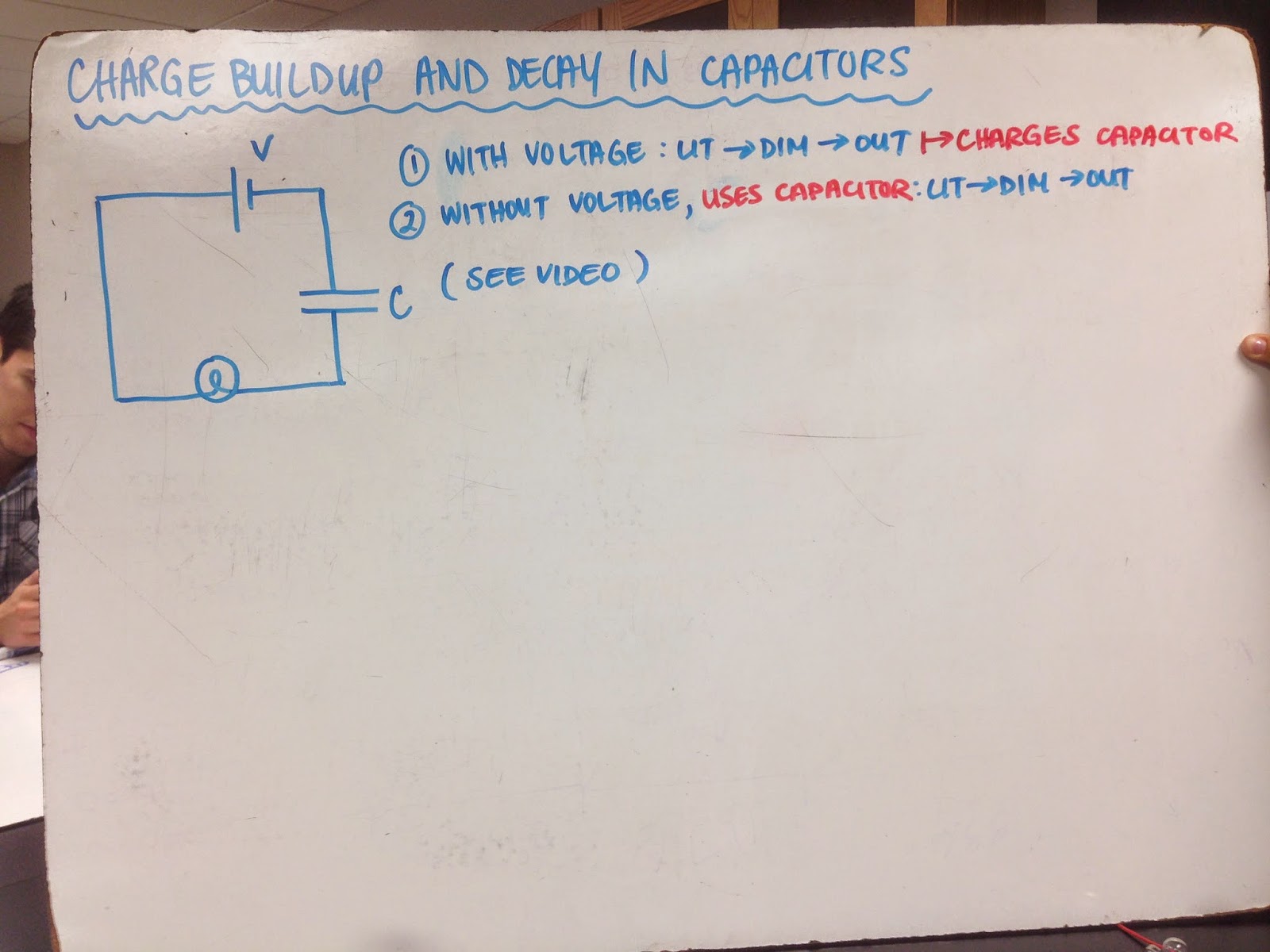

A Capacitance Puzzle

Two separate capacitors each of charge .47 F were each connected to a voltage source one with voltage 3.0 V and the other with voltage 4.5V.  Then the capacitors were unhooked from their batteries and hooked to eachother without being discharged.  We predicted that the voltage across the two would end up being an average of the two voltages.  A system of equations were used to solve this problem and we know that when there is no discharge that the final sum of the charges on the two capacitors is actually the average sum (like an equilibrium point).  We solved for the voltage in the final set up where the capacitors were connected to one another and solved the value to be 3.74.  We then measure the actual voltage between the two capacitors with a multimeter which was found to be 3.94 and found that there was a 5.8 % error between the two numbers probably due to the fact that the capacitors we used when measuring the voltage with the multimeter were .56 F not .47 F.

Quantitative Measurements on an RC System

set up

First we measured the voltage across a charged capacitor as a function of time when a carbon resistor has been placed ina circuit with it.  With the voltage source connected, the graph rises and the levels off and then when the voltage source is disconnected the voltage begins to drop.  (These graphs can be seen on whiteboard) We fit an equation for these graphs and found that they are slightly different for when the voltage source is connected (charging) and when the voltage source is disconnected (discharging).  For the charging capacitor, the voltage equation is A(1-e^(-cb)) and for the discharging capacitor the voltage equation is Ae^(-cb).   After doing unit analysis, it can be seen that A is the max voltage, and cb is equal to t/RC.  Using the data from the graphs, the experimental value for t/RC was -.3620 for the charging capacitor and .3571 for the discharging capacitor.  We calculated the actual value for t/RC with the equipment we used and found it to be .4.  We found that there was a 9.97 and 11.3 % error respectively.

graphs